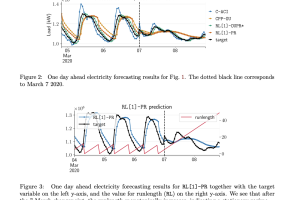
The inability to linearly classify XOR has motivated much of deep learning. We revisit this age-old problem and show that linear classification of XOR is indeed possible. Instead of separating data between halfspaces, we propose a slightly different paradigm, equality separation, that adapts the SVM objective to distinguish data within or outside the margin. Our classifier can then be integrated into neural network pipelines with a smooth approximation. From its properties, we intuit that equality separation is suitable for anomaly detection. To formalize this notion, we introduce closing numbers, a quantitative measure on the capacity for classifiers to form closed decision regions for anomaly detection. Springboarding from this theoretical connection between binary classification and anomaly detection, we test our hypothesis on supervised anomaly detection experiments, showing that equality separation can detect both seen and unseen anomalies.