We propose a framework to tackle table understanding tasks, where we train LLMs to outline their reasoning step by step, updating a given table iteratively to reflect each part of a thought process. This enables the LLM to transform the table into simpler and more manageable segments so that it can understand and analyze each part of the table in depth.
People use tables every day to organize and interpret complex information in a structured, easily accessible format. Due to the ubiquity of such tables, reasoning over tabular data has long been a central topic in natural language processing (NLP). Researchers in this field have aimed to leverage language models to help users answer questions, verify statements, and analyze data based on tables. However, language models are trained over large amounts of plain text, so the inherently structured nature of tabular data can be difficult for language models to fully comprehend and utilize.
Recently, large language models (LLMs) have achieved outstanding performance across diverse natural language understanding (NLU) tasks by generating reliable reasoning chains, as shown in works like Chain-of-Thought and Least-to-Most. However, the most suitable way for LLMs to reason over tabular data remains an open question.
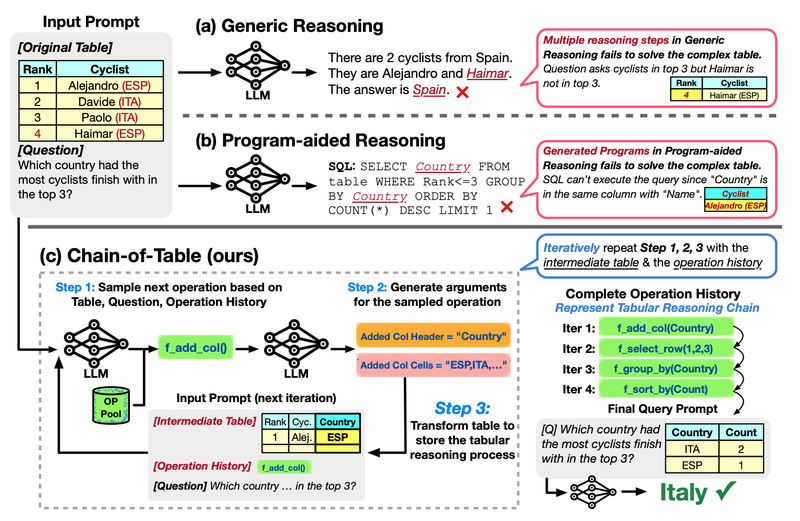
In “Chain-of-Table: Evolving Tables in the Reasoning Chain for Table Understanding”, we propose a framework to tackle table understanding tasks, where we train LLMs to outline their reasoning step by step, updating a given table iteratively to reflect each part of a thought process, akin to how people solve the table-based problems. This enables the LLM to transform the table into simpler and more manageable segments so that it can understand and analyze each part of the table in depth. This approach has yielded significant improvements and achieved new state-of-the-art results on the WikiTQ, TabFact, and FeTaQA benchmarks. The figure below shows the high-level overview of the proposed Chain-of-Table and other methods.
Given a complex table where a cyclist’s nationality and name are in the same cell, (a) generic, multi-step reasoning is unable to provide the correct answer (b) program-aided reasoning generates and executes programs (e.g., SQL queries) to deliver the answer, but falls short in accurately addressing the question. In contrast, (c) Chain-of-Table iteratively samples a chain of operations that effectively transform the complex table into a version specifically tailored to the question.
Chain-of-Table
In Chain-of-Table, we guide LLMs using in-context learning to iteratively generate operations and to update the table to represent its reasoning chain over tabular data. This enables LLMs to dynamically plan the next operation based on the results of previous ones. This continuous evolution of the table forms a chain, which provides a more structured and clear representation of the reasoning process for a given problem and enables more accurate and reliable predictions from the LLM.
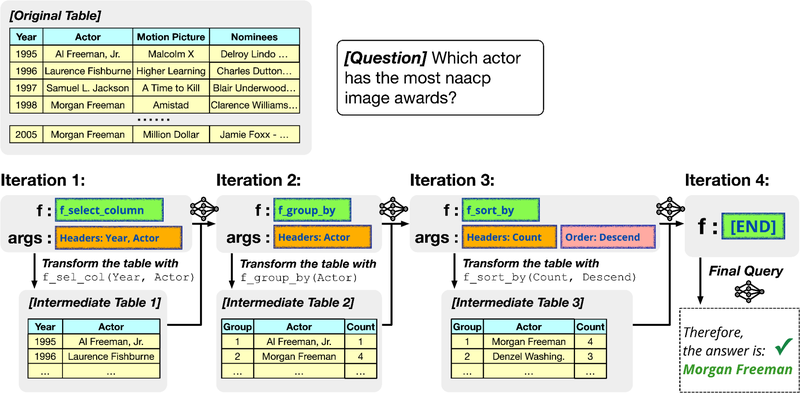
For example, when asked, “Which actor has the most NAACP image awards?” the Chain-of-Table framework prompts an LLM to generate tabular operations mirroring tabular reasoning processes. It first identifies the relevant columns. Then, it aggregates rows based on shared content. Finally, it reorders the aggregated results to yield a final table that clearly answers the posed question.
These operations transform the table to align with the question presented. To balance performance with computational expense on large tables, we construct the operation chain according to a subset of tabular rows.. Meanwhile, the step-by-step operations reveal the underlying reasoning process through the display of intermediate results from the tabular operations, fostering enhanced interpretability and understanding.
Chain-of-Table consists of three main stages. In the first stage, it instructs the LLM to dynamically plan the next operation by in-context learning. Specifically, the prompt involves three components as shown in the following figure:
- The question Q: “Which country had the most cyclists finish in the top 3?”
- The operation history chain: f_add_col(Country) and f_select_row(1, 2, 3).
- The latest intermediate table T: the transformed intermediate table.
By providing the triplet (T, Q, chain) in the prompt, the LLM can observe the previous tabular reasoning process and select the next operation from the operation pool to complete the reasoning chain step by step.
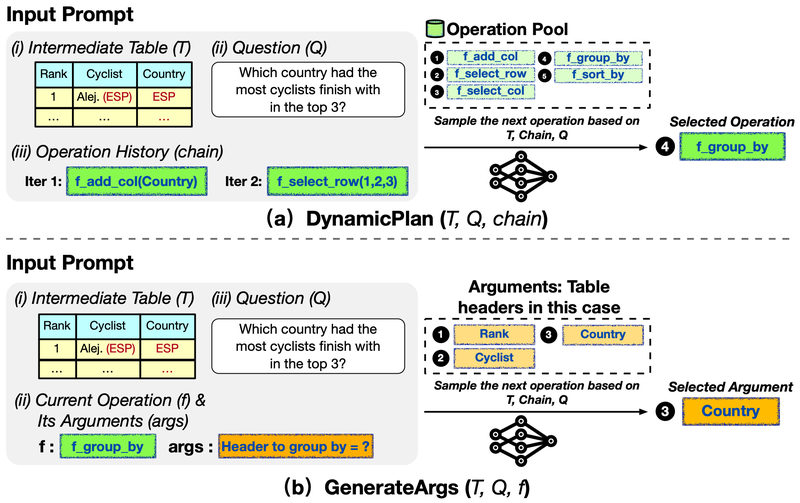
Illustration of how Chain-of-Table selects the next operation from the operation pool and generates the arguments for the operation.(a) Chain-of-Table samples the next operation from the operation pool. (b) It takes the selected operation as input and generates its arguments.
After the next operation f is determined, in the second stage, we need to generate the arguments. As above, Chain-of-Table considers three components in the prompt as shown in the figure: (1) the question, (2) the selected operation and its required arguments, and (3) the latest intermediate table.
For instance, when the operation f_group_by is selected, it requires a header name as its argument.
The LLM selects a suitable header within the table. Equipped with the selected operation and the generated arguments, Chain-of-Table executes the operation and constructs a new intermediate table for the following reasoning.
Chain-of-Table iterates the previous two stages to plan the next operation and generate the required arguments. During this process, we create an operation chain acting as a proxy for the tabular reasoning steps. These operations generate intermediate tables presenting the results of each step to the LLM. Consequently, the output table contains comprehensive information about the intermediate phases of tabular reasoning. In our final stage, we employ this output table in formulating the final query and prompt the LLM along with the question for the final answer.
Experimental setup
We use PaLM 2-S and GPT 3.5 as the backbone LLMs and conduct the experiments on three public table understanding benchmarks: WikiTQ, TabFact, and FeTaQA. WikiTQ and FeTaQA are datasets for table-based question answering. TabFact is a table-based fact verification benchmark. In this blogpost, we will focus on the results on WikiTQ and TabFact. We compare Chain-of-Table with the generic reasoning methods (e.g., End-to-End QA, Few-Shot QA, and Chain-of-Thought) and the program-aided methods (e.g., Text-to-SQL, Binder, and Dater).
More accurate answers
Compared to the generic reasoning methods and program-aided reasoning methods, Chain-of-Table achieves better performance across PaLM 2 and GPT 3.5. This is attributed to the dynamically sampled operations and the informative intermediate tables.
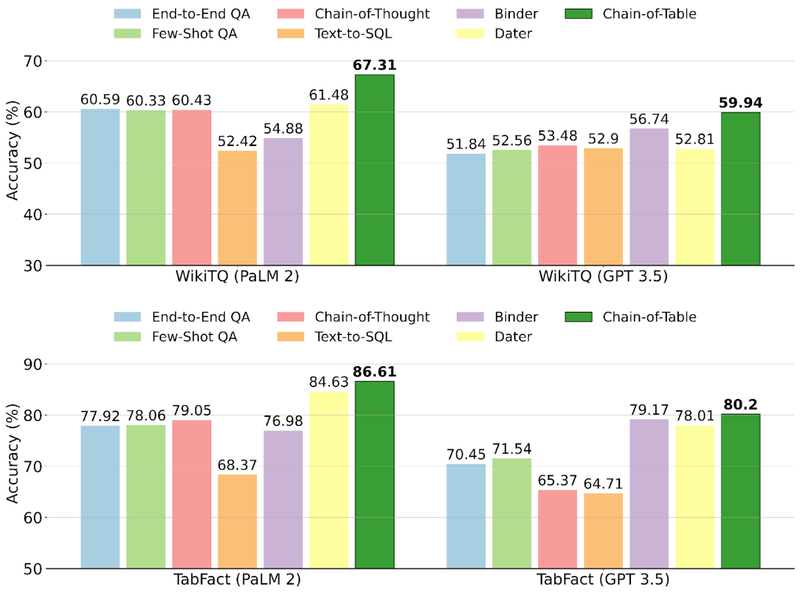
Understanding results on WikiTQ and TabFact with PaLM 2 and GPT 3.5 compared with various models.
Better robustness on harder questions
In Chain-of-Table, longer operation chains indicate the higher difficulty and complexity of the questions and their corresponding tables. We categorize the test samples according to their operation lengths in Chain-of-Table. We compare Chain-of-Table with Chain-of-Thought and Dater, as representative generic and program-aided reasoning methods. We illustrate this using results from PaLM 2 on WikiTQ.
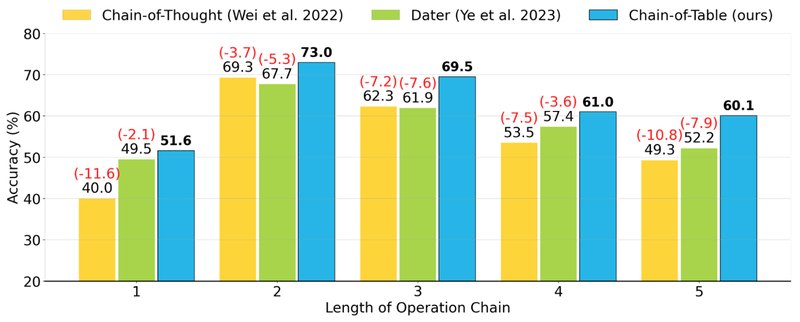
Performance of Chain-of-Thought, Dater, and the proposed Chain-of-Table on WikiTQ for questions that require an operation chain of varying lengths. Our proposed atomic operations significantly improve performance over generic and program-aided reasoning counterparts.
Notably, Chain-of-Table consistently surpasses both baseline methods across all operation chain lengths, with a significant margin up to 11.6{7df079fc2838faf5776787b4855cb970fdd91ea41b0d21e47918e41b3570aafe} compared with Chain-of-Thought, and up to 7.9{7df079fc2838faf5776787b4855cb970fdd91ea41b0d21e47918e41b3570aafe} compared with Dater. Moreover, the performance of Chain-of-Table declines gracefully with increasing number of operations compared to other baseline methods, exhibiting only a minimal decrease when the number of operations increases from four to five.
Better robustness with larger tables
We categorize the tables from WikiTQ into three groups based on token number: small (<2000 tokens), medium (2000 to 4000 tokens) and large (>4000 tokens). We then compare Chain-of-Table with Dater and Binder, the two latest and strongest baselines.
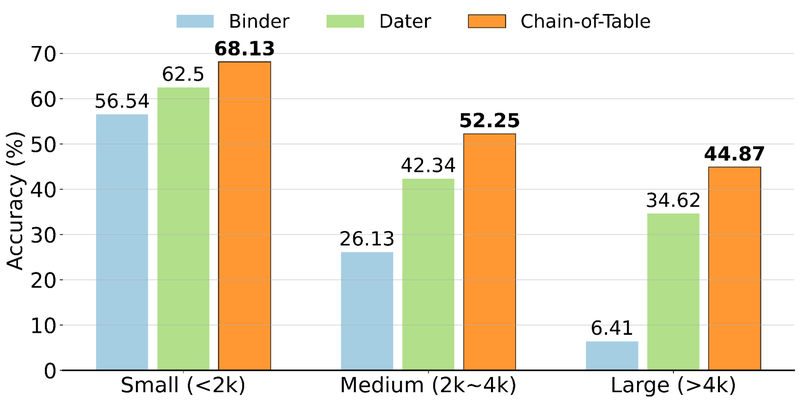
Performance of Binder, Dater, and the proposed Chain-of-Table on small (<2000 tokens), medium (2000 to 4000 tokens), and large (>4000 tokens) tables from WikiTQ. We observe that the performance decreases with larger input tables while Chain-of-Table diminishes gracefully, achieving significant improvements over competing methods. (As above, underlined text denotes the second-best performance; bold denotes the best performance.)
As anticipated, the performance decreases with larger input tables, as models are required to reason through longer contexts. Nevertheless, the performance of the proposed Chain-of-Table diminishes gracefully, achieving a significant 10+{7df079fc2838faf5776787b4855cb970fdd91ea41b0d21e47918e41b3570aafe} improvement over the second best competing method when dealing with large tables. This demonstrates the efficacy of the reasoning chain in handling long tabular inputs.
Conclusion
Our proposed Chain-of-Table method enhances the reasoning capability of LLMs by leveraging the tabular structure to express intermediate steps for table-based reasoning. It instructs LLMs to dynamically plan an operation chain according to the input table and its associated question. This evolving table design sheds new light on the understanding of prompting LLMs for table understanding.
Acknowledgements
This research was conducted by Zilong Wang, Hao Zhang, Chun-Liang Li, Julian Martin Eisenschlos, Vincent Perot, Zifeng Wang, Lesly Miculicich, Yasuhisa Fujii, Jingbo Shang, Chen-Yu Lee, Tomas Pfister. Thanks to Chih-Kuan Yeh and Sergey Ioffe for their valuable feedback.